Сколько литров воды в 1 кубе
Не пугайтесь, мы не начнем заново проходить школьный курс физики. Вместо того, чтобы считать, сколько литров в кубометре воды, вы познакомитесь с «ведрической» системой измерения и узнаете, как она помогла моей семье начать экономить.
Куб воды – это сколько литров?
Скажете, что тут непонятного? В 1 кубе 1000 литров воды, каждый школьник это знает. Ну, во-первых, не каждый (к сожалению). Мне встречались весьма неглупые люди, считавшие, что кубометр состоит из 100 литров. Некоторые выдавали еще более экзотические версии.
Во-вторых, многие путают объем и вес, считая, что количество литров горячей, холодной и дистиллированной воды в 1 кубе будет отличаться. Наверное, причина в том, что на обратной стороне школьных тетрадей вместо таблицы единиц стали печатать фотки Джастина Бибера.
Но речь не о пробелах в образовании, а о том, как эту информацию можно использовать для экономии семейного бюджета. Для этого мы попробуем перевести абстрактный кубометр в более понятные единицы. Вот несколько примеров, дающих представление о том, сколько литров в кубе воды и как их можно израсходовать:
сделать 14 стирок в машине-автомат;
30 раз принять душ;
сделать 111 смываний в туалете.
Правда, так нагляднее? Сразу видно, из чего состоят и куда деваются эти самые кубометры. При желании, список можно продолжить до бесконечности.
Начните экономить литры, а не кубы
Многие удивляются, узнав наведенные выше цифры. Это доказывает, что проблема экономии является, в некоторой степени, психологической. Нам трудно представить, сколько литров воды утекает, пока мы чистим зубы или моем посуду. Ведь мы привыкли измерять ее кубами, которые видим в платежке за коммуналку. А подобные примеры дают нам представление о реальном объеме потребляемой воды.
Как приучить себя и других членов семьи мыслить категориями литров, а не кубов? После некоторых раздумий и бесполезных попыток изменить ситуацию «мирным путем», я поступил следующим образом. Теплым летним днем мы отправились на уик-энд в деревню, к бабушке…
Сразу после нашего приезда у нее неожиданно «сломался» насос в колодце. Не оставалось ничего другого, как прицепить ведро и доставать воду по-старинке, с помощью «корбы». Кто не знает, это примерно вот такая стремная конструкция:
Так вот, за неполных два дня, вчетвером мы израсходовали 10 ведер воды. Сколько литров в ведре, думаю, все знают – 10. После этого я «починил» насос и открыл суть эксперимента. А уже дома мы произвели несложные подсчеты.
На тот момент наш среднемесячный расход воды составлял 10 кубов на троих, то есть, 1000 ведер. Делим на 30 дней, получаем 33 ведра в день, по 11 на человека. Как же у нас получалось два дня вчетвером(!) «укладываться» в 5 ведер?
Да, у бабушки мы не занимались стиркой и пользовались, пардон «удобствами во дворе». Однако, не последнюю роль в снижении расхода воды сыграло то, что для ее получения нужно было совершить дополнительное действие, а не просто повернуть кран. Добывание каждого ведра «вручную» стимулирует к экономии похлеще всякого счетчика.
Придя к такому выводу, первой мыслью было – отказаться от водопровода и вырыть возле подъезда колодец. Однако, потом решили не ударяться в крайности, ограничившись введением «ведрической» системы измерения. Теперь на вопрос «сколько литров воды в 1 кубе», дочка отвечает не «1000 литров», а «100 ведер». Нехитрые вычисления показали, что одно ведро воды соответствует:
1 минуте открытого крана во время умывания или чистки зубов;
смыву унитаза большой кнопкой;
и так далее…
Уж не знаю, что больше подействовало: более наглядное представление расхода или аргумент «кто не экономит воду – тот не жалеет бабушку». Однако, уже в следующем месяце мы использовали на 2 куба меньше. Как-то, само по себе, сократилось проводимое под душем время, а на раковине появился стакан для чистки зубов…
Причем, что характерно, только после этого мы всерьез подошли к другим способам экономии воды. Это позволило сократить потребление еще на 1 куб. Сейчас мы расходуем 6,5-7 кубов воды в месяц, что для семьи из трех человек – вполне нормально.
Сколько килограмм в 1 кубе щебня? Калькулятор
Нерудные материалы продают по цене за 1 кубометр. Знание объема необходимо для расчета стоимости стройматериалов, подбора грузовой машины для их перевозки, расчета количества нерудных материалов при обустройстве щебневой подушки под фундамент и т.д. Но для приготовления бетона и строительных смесей нужно знать, сколько килограмм в 1 кубе щебня.
Калькулятор
Масса кубического метра щебеня
| 1 куб щебня | Вес кг |
|---|---|
| гравийный щебень | 1350 |
| гравийный щебень 5-20 | 1430 |
| гравийный щебень 20-40 | 1540 |
| гравийный щебень 40-70 | 1650 |
| гранитный щебень | 1390 |
| гранитный щебень 5-20 | 1350 |
| гранитный щебень 20-40 | 1380 |
| гранитный щебень 40-70 | 1440 |
| известняковый щебень | 1300 |
| известняковый щебень 5-20 | 1370 |
| известняковый щебень 20-40 | 1410 |
| известняковый щебень 40-70 | 1470 |
На нашем сайте вы можете рассчитать, сколько килограмм в 1 м3 (кубе) щебня с помощью калькулятора и таблицы.
Как определить вес щебенки?
Делают это по формуле:
p = m : V, где
p – насыпная плотность,
m – масса вещества,
V – объем сосуда.
Например, если в мерной емкости объемом 50 л умещается 69 кг гранитного щебня с размером зерен 20–40 мм, можно вычислить примерную насыпную плотность:
69 кг : 0,05 куб. м = 1380 кг/куб. м
Такова насыпная плотность материала в сухом, неуплотненном состоянии. Трамбовать щебенку и взвешивать ее влажной нецелесообразно, поскольку плотность сильно возрастет и не будет отражать реальные физико-механические свойства материала.
Масса 1 м3 щебня
Вес 1 куб. м щебенки – это и есть соотношение ее массы к определенному объему. Такое соотношение заранее определено, ведь перед поступлением партии нерудных материалов в продажу обязательно проводят ее лабораторные испытания, определяют качество материала и значимые характеристики, которые заносят в сопроводительную документацию: сертификаты соответствия, протоколы, паспорта на щебень. Качественные сыпучие материалы всегда соответствуют характеристикам, прописанным в ГОСТ 8269.0-97. Чтобы определить, сколько килограммов в 1 кубометре щебня, используйте приведенную выше таблицу.
Статьи по теме
Доставка нерудных материалов по ЦФО
Позвоните нам!
или оставьте заявку
Сколько тонн в кубе щебня 20-40? Калькулятор
Таблица
| 1 куб щебня | Тонны |
|---|---|
| известняковый щебень 20-40 | 1,41 |
| гранитный щебень 20-40 | 1,38 |
| гравийный щебень 20-40 | 1,54 |
Нерудные материалы с модулем крупности 20–40 мм используют в дорожном строительстве, при обустройстве фундамента, производстве ЖБИ и аэродромных плит. Их продают по цене за кубометр, но в приготовлении строительных смесей важна масса компонентов. Поэтому важно знать, сколько тонн в кубе щебня 20–40!
Как рассчитать?
Масса 1 кубометра материала зависит от размера фракций, вида горной породы и влажности. В идеальных условиях, соответствующих нормам ГОСТ 8267-93 составляет около 4 % до 10 % при хранении на открытых складах без защитных покрытий). Поскольку этот показатель одинаков для всех видов качественных нерудных материалов, при расчетах его редко используют (только в лабораторных условиях, определяя характеристики щебенки из конкретной партии).
Горные породы имеют различную плотность, в связи с чем гравий значительно тяжелее известняка. Поэтому масса куба этих видов щебня не одинакова. Рассчитывают ее по формуле:
p = m : V, где
p – масса 1 куб. м,
m – масса материала,
V – объем заполненного им сосуда.
Для определения примерного веса куба щебенки 20-40 мм возьмем ведро 50 л и заполним до краев известняковым материалом. Взвесим емкость и посчитаем:
64 кг : 0,05 куб. м = 1280 кг/куб. м
При заполнении 12-литрового ведра гравием получим другие показатели:
19,2 кг : 0,012 куб. м =1600 кг/куб. м
Теперь наполним 10-литровое ведро гранитным щебнем 20-40:
13,8 кг : 0,01 куб. м = 1380 кг/куб. м
Мы получили показатели, соответствующие насыпной плотности этих материалов. Данная характеристика отражает объемный вес материала с учетом пустот между его частицами. Поскольку рассчитывать массу кубометра следует, помня о наличии воздуха между зернами. При этом чем крупнее зерна, тем больше пустот между ними. Поэтому масса куба щебня с частицами, размеры которых отличаются практически вдвое, будет не столь существенной.
Как узнать массу куба щебня?
Произвести необходимые расчеты можно в домашних условиях, но для этого нужно закупит нерудный материал в малом объеме. В противном случае проводить замеры придется прямо на предприятии, которое поставляет щебенку. Но это не слишком удобно и надежно, ведь при производстве таких расчетов погрешность очень велика. Для точности следует запросить у поставщика сопроводительные документы (паспорт или сертификат), в которых будет значение насыпной плотности, вычисленное в лаборатории. А вычислить, сколько тонн в 1 кубическом метре щебня фракции 20-40, не выходя из дома или офиса, поможет калькулятор на нашем сайте!
Доставка нерудных материалов по ЦФО
Позвоните нам!
или оставьте заявку
Куб (алгебра) — Википедия
Материал из Википедии — свободной энциклопедии
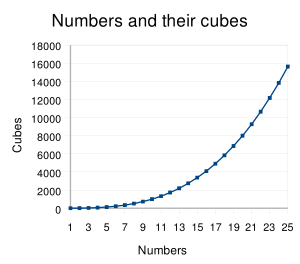y=x³, при целых значениях x от 1 до 25Кубом числа x{\displaystyle x} называется результат возведения числа в степень 3, то есть произведение трёх множителей, каждый из которых равен x.{\displaystyle x.} Эта арифметическая операция называется «возведением в куб», её результат обозначается x3{\displaystyle x^{3}}:
- x3=x⋅x⋅x{\displaystyle x^{3}=x\cdot x\cdot x}
Для возведения в куб обратной операцией является извлечение кубического корня. Геометрическое название третьей степени «куб» связано с тем, что античные математики рассматривали значения кубов как кубические числа, особый вид фигурных чисел (см. ниже), поскольку куб числа x{\displaystyle x} равен объёму куба с длиной ребра, равной x{\displaystyle x}.
Последовательность кубов неотрицательных чисел начинается числами[1]:
- 0, 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744, 3375, 4096, 4913, 5832, 6859, 8000, 9261, 10648, 12167, 13824, 15625, 17576, 19683, 21952, 24389, 27000, 29791, 32768, 35937, 39304, 42875, 46656, 50653, 54872, 59319, 64000, 68921, 74088, 79507, 85184, 91125, 97736, 103823, 110592, 117649, 125000, 132651, 140608, 148877, 157464, 166375, 175616, 185193, 195112, 205379, 216000, 226981, 238328…
Сумма кубов первых n{\displaystyle n} положительных натуральных чисел вычисляется по формуле:
- ∑i=1ni3=13+23+33+…+n3=(n(n+1)2)2{\displaystyle \sum _{i=1}^{n}i^{3}=1^{3}+2^{3}+3^{3}+\ldots +n^{3}=\left({\frac {n(n+1)}{2}}\right)^{2}}
Вывод формулы[править | править код]
Формулу суммы кубов можно вывести, используя таблицу умножения и формулу суммы арифметической прогрессии[2]. Рассматривая в качестве иллюстрации метода две таблицы умножения 5×5, проведём рассуждения для таблиц размером n×n.
|
|
Сумма чисел в k-ой (k=1,2,…) выделенной области первой таблицы:
- k2+2k∑l=1k−1l=k2+2kk(k−1)2=k3{\displaystyle k^{2}+2k\sum _{l=1}^{k-1}l=k^{2}+2k{\frac {k(k-1)}{2}}=k^{3}}
А сумма чисел в k-ой (k=1,2,…) выделенной области второй таблицы, представляющих собой арифметическую прогрессию:
- k∑l=1nl=kn(n+1)2{\displaystyle k\sum _{l=1}^{n}l=k{\frac {n(n+1)}{2}}}
Суммируя по всем выделенным областям первой таблицы, получаем такое же число, как и суммируя по всем выделенным областям второй таблицы:
- ∑k=1nk3=∑k=1nkn(n+1)2=n(n+1)2∑k=1nk=(n(n+1)2)2{\displaystyle \sum _{k=1}^{n}k^{3}=\sum _{k=1}^{n}k{\frac {n(n+1)}{2}}={\frac {n(n+1)}{2}}\sum _{k=1}^{n}k=\left({\frac {n(n+1)}{2}}\right)^{2}}
- В десятичной записи куб может кончаться на любую цифру (в отличие от квадрата)
- В десятичной записи две последние цифры куба могут быть 00, 01, 03, 04, 07, 08, 09, 11, 12, 13, 16, 17, 19, 21, 23, 24, 25, 27, 28, 29, 31, 32, 33, 36, 37, 39, 41, 43, 44, 47, 48, 49, 51, 52, 53, 56, 57, 59, 61, 63, 64, 67, 68, 69, 71, 72, 73, 75, 76, 77, 79, 81, 83, 84, 87, 88, 89, 91, 92, 93, 96, 97, 99. Зависимость предпоследней цифры куба от последней можно представить в виде следующей таблицы:
последняя
цифрапредпоследняя
цифра0 0 5 2, 7 4, 8 чётная 2, 6 нечётная 1, 3, 7, 9 любая
«Кубическое число» Qn=n3{\displaystyle Q_{n}=n^{3}} исторически рассматривалось как разновидность пространственных фигурных чисел. Его можно представить как разность квадратов последовательных треугольных чисел[3]Tn{\displaystyle T_{n}}:
- Qn=(Tn)2−(Tn−1)2,n⩾2{\displaystyle Q_{n}=(T_{n})^{2}-(T_{n-1})^{2},n\geqslant 2}
- Следствие: сумма первых n{\displaystyle n} кубических чисел равна квадрату n{\displaystyle n}-го треугольного числа:
- Q1+Q2+Q3+⋯+Qn=(Tn)2{\displaystyle Q_{1}+Q_{2}+Q_{3}+\dots +Q_{n}=(T_{n})^{2}}
Разность между двумя соседними кубическими числами есть центрированное шестиугольное число.
- Следствие: сумма первых n{\displaystyle n} центрированных шестиугольных чисел есть кубическое число Qn{\displaystyle Q_{n}}[3].
Выражение кубического числа через тетраэдральные[3]Πn(3){\displaystyle \Pi _{n}^{(3)}}:
- Qn=Πn(3)+4Πn−1(3)+Πn−2(3){\displaystyle Q_{n}=\Pi _{n}^{(3)}+4\Pi _{n-1}^{(3)}+\Pi _{n-2}^{(3)}}, где n>2.{\displaystyle n>2.}
Одна из «гипотез Поллока» (1850 год): каждое натуральное число представимо как сумма не более девяти кубических чисел. Доказана в начале XX века. Обычно достаточно семи кубов, но 15 чисел требуют восьми (15, 22, 50, 114, 167, 175, 186, 212, 231, 238, 303, 364, 420, 428, 454, последовательность A018889 в OEIS), а двум числам нужны все девять: 23 и 239. Если, кроме сложения, допускать вычитание, то достаточно и пяти кубов (возможно, что даже четырёх, но это пока не доказано)[4].
Производящая функция кубических чисел имеет вид[3]:
- f(x)=x(x2+4x+1)(x−1)4;|x|<1{\displaystyle f(x)={\frac {x(x^{2}+4x+1)}{(x-1)^{4}}};\quad |x|<1}
- Виленкин Н. Я., Шибасов Л. П. Шибасова 3. Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия. — М.: Просвещение, 1996. — С. 30. — 320 с. — ISBN 5-09-006575-6.
- Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — 376 с.
- Деза Е., Деза М. Фигурные числа. — М.: МЦНМО, 2016. — 349 с. — ISBN 978-5-4439-2400-7.