Площадь купола формула: Площадь поверхности купола — Циклопедия – Площадь поверхности шарового сегмента | Формулы и расчеты онлайн

Содержание

Онлайн калькулятор: Сегмент шара

Сегмент шара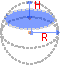

Сферический сегмент

Шаровым сегментом называется часть шара, отсеченная от него плоскостью.

Формулы:
— площадь боковой поверхности
— площадь основания
— формула объема

Сегмент шара

Точность вычисления

Знаков после запятой: 5

Площадь боковой поверхности

Площадь основания

Площадь поверхности

save Сохранить extension Виджет

Слой шара Сферический слой
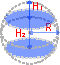
Шаровой слой — часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.
Формулы:
— площадь боковой поверхности
— объем

Шаровой слой
Точность вычисления
Знаков после запятой: 5
Площадь боковой поверхности

Площадь поверхности

save Сохранить extension Виджет
Объём купола — Циклопедия
Купол с α Купол с α>π/2
Объём купола — это объём, ограниченный образующей сегмента, вращающегося вокруг оси, проходящей через одну вершину сегмента (под острым углом к диаметру основания сегмента), и плоскостью перпендикулярной оси вращения.

Под куполом будем подразумевать тело, ограниченное образующей сегмента, вращающегося вокруг оси, проходящей через одну вершину сегмента (под острым углом к диаметру основания сегмента), и плоскостью перпендикулярной оси вращения.
Введём обозначения:
R — радиус образующей дуги окружности;
r — радиус основания купола;
ρ — расстояние от основания купола до горизонтальной оси, проходящей через центр образующей окружности;
с — расстояние от центра образующей дуги окружности до вертикальной оси купола;
h — высота купола;
α — угол между радиусами образующей дуги окружности, соединяющими центр с краями образующего сегмента;

V_куп — объём купола.
[править] Объём купола при α<π/2
[править] Объём купола при α>π/2
[править] Объём купола при α<π/2
[править] Объём купола при α>π/2
[править] Другие формулы
Формулы площадей всех основных фигур
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание

c — равные боковые стороны
α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):

2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции

Формула площади равнобокой трапеции через радиус вписанной окружности, (

S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции

c — боковая сторона
α, β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b — верхнее основание
a — нижнее основание
h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S):

Площадь купола — Square cupola
В геометрии , то квадратный купол , который иногда называют меньший купол , является одним из твердых веществ Johnson ( J ₄ ). Он может быть получен в виде ломтика ромбокубооктаэдра . Как и во всех cupolae , базовый полигон имеет в два раза больше ребер и вершин , как сверху; В этом случае базовый полигон представляет собой восьмиугольник .
Джонсон твердого веществом является одним из 92 строго выпуклых многогранников , которые имеют регулярное лицо , но не являются однородными (то есть, они не являются Платоновыми тела , Архимед твердых частиц , призмы или антипризмы ). Они были названы Норман Джонсон , который первым в списке этих многогранников в 1966 году.

Формулы
Следующие формулы для объема , площади поверхности , и описанной окружности могут быть использованы , если все лица являются регулярными , с длиной ребром а :
Взнак равно(1+223)a3≈1,94281 …a3{\ Displaystyle V = (1 + {\ гидроразрыва {2 {\ SQRT {2}}} {3}}) а ^ {3} \ около 1,94281 … а ^ {3}}
Aзнак равно(7+22+3)a2≈11,5605 …a2{\ Displaystyle А = (7 + 2 {\ SQRT {2}} + {\ SQRT {3}}) а ^ {2} \ около 11,5605 … а ^ {2}}
Сзнак равно(125+22)a≈1,39897 …a{\ Displaystyle С = ({\ гидроразрыва {1} {2}} {\ SQRT {5 + 2 {\ SQRT {2}}}}) а \ около 1,39897 … а}
Связанные многогранники и Соты
Другой выпуклый cupolae
двойной многогранник
Двойные квадратного купол имеет 8 треугольные и 4 лица змея:
Двойной квадратный купол Net двойного

Скрещенные квадратный купол
Пересекли квадратный купол является одним из невыпуклых твердых Джонсоных изоморфов, будучи топологический идентична выпуклым квадратный купол. Он может быть получен в виде ломтика невынуклого большого ромбокубооктаэдра или quasirhombicuboctahedron, аналогично тому , как квадратный купол может быть получен в виде ломтика ромбокубооктаэдра. Как и во всех cupolae , базовый полигон имеет в два раза больше ребер и вершин , как сверху; В этом случае базовый полигон является октаграммой .
Это может рассматриваться как купол с ретроградным квадратным основанием, так что квадраты и треугольники соединить через основания в обратном направлении к квадратному куполу, следовательно, пересекающиеся друг с другом.
Соты
Квадратный купол является компонентом нескольких неоднородных пространственных решеток заполнения:
Рекомендации
внешняя ссылка
<img src=»https://en.wikipedia.org//en.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
как расчитать площадь купола мечети, может есть формула?
Любая твердотелка типа КОМПАС или Inventor позволяет вычислять в т. ч. площади. Просто модель нужно построить. Для этого надо эту кривую вокруг оси провращать. Всего одна операция и можно нажимать кнопочку «вычислить площадь. Естественно, должны знать размеры основания, башни и навершия купола. Основную проблему составят размеры так называемой башни (отмечено стрелками) «<img src=»//otvet.imgsmail.ru/download/c6ff14bffe4b4df9df63970f585fb609_i-145.jpg» > Облегченный КОМПАС отсюда скачать можно. <a rel=»nofollow» href=»http://softsearch.ru/programs/203-109-kompas-3d-lt-download.shtml» target=»_blank»>http://softsearch.ru/programs/203-109-kompas-3d-lt-download.shtml</a> Для грубой оценки можно допустить, что купол — половина эллипсоида. Тогда площадь эллипсоида с помощью этого калькулятора вычислить можно <a rel=»nofollow» href=»http://www.planetcalc.ru/149/» target=»_blank»>http://www.planetcalc.ru/149/</a>
<a rel=»nofollow» href=»/» title=»12460364:##:showthread.php?t=18813″ target=»_blank» >[ссылка заблокирована по решению администрации проекта]</a> (ссылки, примеры) <a rel=»nofollow» href=»http://www.npoik.ru/lib/?category=catalog&idtov=75″ target=»_blank»>http://www.npoik.ru/lib/?category=catalog&idtov=75</a> (книга: Купольные конструкции: формообразование, расчет, конструирование, повышение эффективности. Для доступа в библиотеку нужна регистрация) <a rel=»nofollow» href=»http://dwg.ru/dnl/2516″ target=»_blank»>http://dwg.ru/dnl/2516</a> (Книга: Купола. Расчет и проектирование. 1973 г. Лепницкий М. Е. В книге рассматриваются разнообразные купольные оболочки: купола-оболочки, ребристые купола, ребристо-кольцевые купола, сетчатые купола — описание, расчеты и т. д. Можно свободно скачать) .
Бабушка подходит к наркоману и спрашивает: «Сынок, как мне найти площадь Ильича? » Тот почесал тыковку и отвечает: «Да все элементарно бабуля — надо длинну Ильича умножить на ширину Ильича! » :))
Площадь купола формула — Портал о стройке

Source: www.freechemistry.ru

Читайте также

ПЛОЩАДЬ ПЛОСКИХ ФИГУР

прямоугольник S = a × b, где a, b — строны прямоугольника
треугольник S = a × h/2, где a, h — строна и высота треугольника
параллелограмм S = a × h, где a, h — строна и высота параллелограмма
трапеция S = ( a + b ) h/2, где a, b — основания; h — высота трапеции
окружность S = πR², где R — радиус окружности
эллипс S = π × a b, где a, b — большая и малая полуоси эллипса

ПЛОЩАДЬ ПОВЕРХНОСТИ ОБЪЕМНЫХ ФИГУР

параллепипед
S = 2(ab+bc+ac), где a, b, c — ребра параллепипеда
конус S = πRl + πR² , где R — радиус окружности; l — длина образующей
круговой цилиндр S = 2πR(h+R) , где R — радиус окружности; h — высота
сфера (шар) S = 4πR² , где R — радиус сферы
тетраэдр S = 1,7321 a² , где а — ребро
октаэдр S = 3,4641 a², где а — ребро
додекаэдр S = 20,6457 a² , где а — ребро
икосаэдр S = 8,6603 a², где а — ребро

ОБЪЕМ ФИГУР

параллепипед V = a × b × с, где a, b, c — ребра параллепипеда
конус V = (1/3)πR², где R — радиус окружности; h — высота
круговой цилиндр V = πR² × h , где R — радиус окружности; h — высота
сфера (шар) V = (4/3)πR³ , где R — радиус сферы
эллипсоид V = (4/3)πabc, где a, b, c — полуоси эллипса
тетраэдр V = 0,1179 a³, где а — ребро
октаэдр V = 0,4714 a³, где а — ребро
додекаэдр V = 7,6631 a³ , где а — ребро
икосаэдр V = 2,1817 a³ , где а — ребро

Площадь поверхности сфероида — Циклопедия
Сфероид вытянутый Сфероид сплюснутый
Площадь сфероида — это число, характеризующее сфероид в единицах измерения площади.
Сфероид — это тело, ограниченное эллипсоидом вращения.
Эллипсоид вращения — это поверхность в трёхмерном пространстве, образованная вращением эллипса вокруг одной из его осей.
[править] Виды сфероидов
вытянутый;
сплюснутый;
нормальный.
Вытянутый сфероид ограничен вытянутым эллипсоидом вращения.
Вытянутый эллипсоид вращения — это геометрическое место точек пространства, для которых сумма расстояний до двух заданных точек (фокусов) постоянна (равна большой оси). Вытянутый эллипсоид вращения получается вращением эллипса вокруг большой оси. У вытянутого эллипсоида вращения одна большая ось и две малые оси.
Сплюснутый сфероид ограничен сплюснутым эллипсоидом вращения.
Сплюснутый эллипсоид вращения — это геометрическое место точек пространства, для которых сумма расстояний до ближайшей и до наиболее удалённой точки заданной окружности постоянна (равна малой оси). Сплюснутый эллипсоид вращения получается вращением эллипса вокруг малой оси. У сплюснутого эллипсоида вращения две большие оси и одна малая ось.
Нормальный сфероид — это шар (ограничен сферой).
Введём обозначения:
a — большая полуось;
b — малая полуось;
S_{сфер.вытян} — площадь вытянутого сфероида.
S_{сфер.сплюсн} — площадь сплюснутого сфероида.
[править] Формула 1
[править] Формула 2
[править] Другие формулы